

+ នៅក្នុងប្រព័ន្ធព្រះអាទិត្យភពទាំងអស់មានចលនាវិលជុំវិញព្រះអាទិត្យនៅក្នុងទិសដៅតែមួយគឺបញ្ច្រាសនឹងទ្រនិចនាឡិកា។
+ យើងក៏បានដឹងផងដែរថា
ភពនីមួយៗមានចម្ងាយពីព្រះអាទិត្យ ទម្រង់គន្លង
និងរយៈពេលវិល១ជុំវិញព្រះអាទិត្យយ៉ាងជាក់ លាក់។
+ រង្វិលខ្ញាល់ គឺជាចលនារបស់ភពវិលជុំវិញអ័ក្ស
ឬវិលជុំវិញខ្លួនឯង។
+ បាតុភូតនៃរង្វិលខ្ញាល់នេះបង្កើតឱ្យមាន ថ្ងៃ
និងយប់ ដូចដែលយើងបានឃើញនៅលើភពផែនដី។
+ ភពទាំងអស់មានទិសដៅរង្វិលខ្ញាល់ មិនដូចគ្នាទេ។
+ ជាក់ស្តែង ភពសុក្រ និងភពអ៊ុយរ៉ានុសវិលជុំវិញខ្លួនឯងផ្ទុយពីភពដទៃទៀត។
+ រង្វិលជុំ គឺជាចលនារបស់ភពធ្វើដំណើរវិលជុំវិញព្រះអាទិត្យតាមគន្លង។
+ នៅភពផែនដី ចលនារង្វិលជុំបង្កើតឱ្យមានរដូវ។
ជាទូទៅយើងដឹងថា ផែនដីវិលជុំវិញព្រះអាទិត្យ១ជុំ ស្មើនឹង ៣៦៥ថ្ងៃ និង៦ម៉ោង។

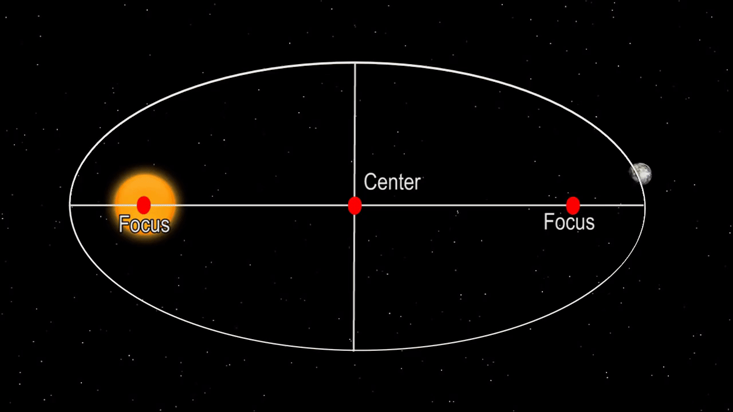
+ ច្បាប់ចលនាទី១ ឬទ្រឹស្តីទី១ របស់កេព្លែ (Kepler first law) កំណត់ថា ភពទាំងអស់មានគន្លងជុំវិញព្រះអាទិត្យក្នុងទម្រង់ជាអេលីប ដោយព្រះអាទិត្យមានទីតាំងនៅត្រង់កំណុំមួយ ក្នុងចំណោម កំណុំទាំងពីររបស់អេលីប។
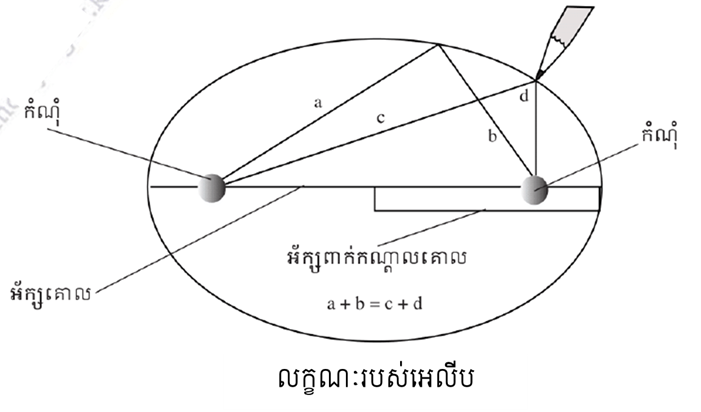
+ នេះមានន័យថាចម្ងាយរវាងភព និងព្រះអាទិត្យមិនមានតម្លៃថេរនោះទេ ផ្ទុយទៅវិញ នៅពេលដែលភពមានចលនាវិលជុំវិញព្រះអាទិត្យ ចម្ងាយរវាងភព និងព្រះអាទិត្យត្រូវប្រែប្រួលជាប់ជាប្រចាំ ទៅតាមគន្លងជាអេលីបរបស់ភព។
+ ច្បាប់ចលនាទី២ ឬទ្រឹស្តីទី២ របស់កេព្លែ (Kepler second law) កំណត់ថា ល្បឿនរបស់ភពជុំវិញព្រះអាទិត្យក៏មិនថេរជាប់ជានិច្ចនោះដែរ ដោយវាត្រូវប្រែប្រួលអាស្រ័យថា តើភពស្ថិតនៅក្បែរព្រះអាទិត្យ ឬឆ្ងាយពីព្រះអាទិត្យ។
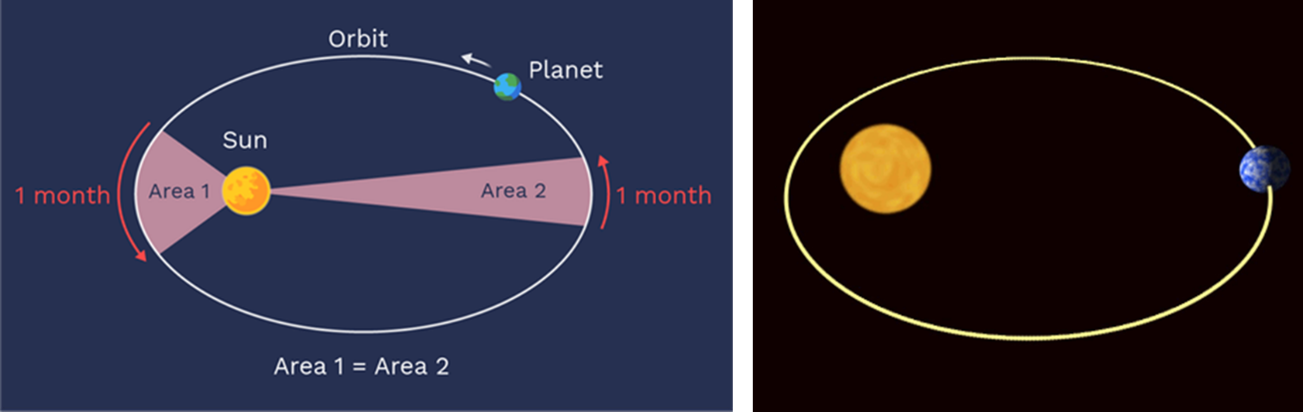
+ ចំណុចដែលភពស្ថិតនៅចម្ងាយជិតបំផុតនឹងព្រះអាទិត្យ
គេហៅថា Perihelion ។
+ ចំណុចដែលភពស្ថិតនៅឆ្ងាយបំផុតពីព្រះអាទិត្យ
គេឲ្យឈ្មោះថា Aphelion ។
+ ដូច្នេះតាមទ្រឹស្តីទី២របស់កេព្ល័រភពមានចលនាវិលជុំវិញព្រះអាទិត្យក្នុងល្បឿនលឿនបំផុតនៅត្រង់ចំណុច
Perihelion ហើយល្បឿនយឺតបំផុតនៅត្រង់ចំណុច Aphelion ។
+ ច្បាប់ចលនាទី ៣ ឬទ្រឹស្តីទី៣ របស់កេព្លែ (Kepler third law) កំណត់ថា
រយៈពេលដែលភពមួយត្រូវធ្វើដំណើរបានពេញមួយជុំព្រះអាទិត្យ គឺអាចយូរ ឬឆាប់
អាស្រ័យទៅលើ ចម្ងាយរវាងភព និងព្រះអាទិត្យ។
+ មានន័យថាភពដែលស្ថិតនៅកាន់តែឆ្ងាយពីព្រះអាទិត្យត្រូវចំណាយពេលកាន់តែយូរដើម្បីអាចធ្វើដំណើរបានមួយជុំព្រះអាទិត្យ។
+ ហេតុដូច្នេះហើយបានជាជាក់ស្តែង
គេសង្កេតឃើញថា៖
- ភពពុធ ដែលជាភពស្ថិតនៅក្បែរព្រះអាទិត្យជាងគេ
អាចធ្វើដំណើរមួយជុំព្រះអាទិត្យ ក្នុងរយៈពេលតែ ៨៨ថ្ងៃ។
- ផែនដីវិលមួយជុំក្នុងរយៈពេល ៣៦៥ថ្ងៃ។
- ចំណែកភពសៅរ៍វិញ
ត្រូវប្រើពេលរហូតដល់ទៅ ១០ ៧៥៩ថ្ងៃ
ពោលគឺ ២៩ឆ្នាំ ទើបអាចធ្វើដំណើរបានមួយជុំ
ព្រះអាទិត្យ។
+ ថ្វីត្បិតនៅពេលនោះ លោក ចូហាន កេព្លែ (Johannes Kepler) ពុំទាន់ដឹងនៅឡើយពីកម្លាំងទំនាញ
ក៏ប៉ុន្តែទ្រឹស្តីទី៣ របស់លោកបានក្លាយជាមូលដ្ឋានគ្រឹះដ៏សំខាន់មួយ សម្រាប់ លោក អ៊ីសាក់
ញូតុន ក្នុងការបង្កើតទ្រឹស្តីទំនាញសកល ផងដែរ។
+ លោក អ៊ីសាក់ ញូតុន គឺជារូបវិទូ ជនជាតិអង់គ្លេស ដែលបង្កើតច្បាប់ទំនាញសកល នៅទសវត្សន៍ឆ្នាំ១៧០០ ។

+ កម្លាំងទំនាញសកល គឺជាសមាមាត្រនៃម៉ាសអង្គទាំងពីរ
ហើយច្រាស់សមាមាត្រនឹងការេទៅនឹងចម្ងាយរវាងអង្គទាំងពីរ។
+ ប្រសិនបើអង្គទាំងពីរធ្វើដំណើរចេញឆ្ងាយពីគ្នា 2ដង
នោះកម្លាំងទំនាញអង្គទាំងពីរនឹងថយចុះតាមរូបមន្ត 2x2=4 ហើយបើចេញឆ្ងាយ 10 នោះស្មើនឹង 10x10=100 ។
+ កម្លាំងទំនាញ រវាងវត្ថុពីរអាស្រ័យទៅនឹងលក្ខណ៖
- ម៉ាសរបស់ទាំងពីរ
- ចម្ងាយរវាងអង្គទាំងពីរ។
+ ជាទូទៅ
ភពដែលនៅជិតព្រះអាទិត្យធ្វើដំណើរលឿនជាងភពនៅឆ្ងាយពីព្រះអាទិត្យ ពីព្រោះ
- ភពដែលនៅជិត
មានគន្លងតូចជាងភពដែលនៅឆ្ងាយព្រះអាទិត្យ
- ភពដែលនៅជិតមានកម្លាំងទំនាញខ្លាំងជាង។
+ ចំណែកឯភពដែលនៅឆ្ងាយពីព្រះអាទិត្យ មានគន្លងធំ
និងកម្លាំងទំនាញខ្សោយ។
+ លោក ញូតុន បានពន្យល់ថា៖ ដោយសារទំនាញ
បើសិនព្រះចន្ទមិនធ្វើចលនាលឿននោះទេព្រះចន្ទគួរតែបុកទង្គិចជាមួយផែនដី
ហើយប្រសិនបើគ្មានទំនាញ នោះព្រះចន្ទនឹងហោះចេញឆ្ងាយពីផែនដី។
+ ភពទាំងអស់បន្តវិលជុំវិញគន្លងព្រះអាទិត្យ
ដោយសារតែ
- កម្លាំងនិចលភាព (ច្បាប់ទី១ របស់ញូតុន)
- កម្លាំងទំនាញរវាងព្រះអាទិត្យ និងភពទាំងនោះ
(ច្បាប់ទី៣ របស់ញូតុន) ។ បញ្ជាក់ថា អង្គទាំងអស់នៅក្នុងសកលទាញគ្នាទៅវិញទៅមក។
+ ទាំងផែនដី
និងភពផ្សេងទៀតនៃប្រព័ន្ធព្រះអាទិត្យរបស់យើង
ផ្លាស់ទីតាមគន្លងរបស់វាជុំវិញព្រះអាទិត្យ។ ល្បឿននៃចលនា
និងគន្លងតាមលំដាប់គ្នាជាក់លាក់។
+ ទំនាញផ្ទៃលើ គឺជារង្វាស់កម្លាំងទំនាញស្ថិតនៅផ្ទៃខាងលើនៃភព
ឬតារានឹង។
+ វាជាសំទុះនៅលើម៉ាសដែលបង្កើតឡើងដោយកម្លាំងទំនាញនៅចំណុចនោះ។
+ ម៉ាស ជារង្វាស់បរិមាណនៃរូបធាតុដែលវត្ថុមួយផ្ទុក
ហើយមានលក្ខណៈថេរ។ ទម្ងន់របស់អង្គអាស្រ័យលើម៉ាស និងសំទុះនៃទំនាញ។
+ រូបមន្តសម្រាប់គណនាទំនាញផ្ទៃលើ៖
