

ជំពូកទី៣ ៖ បន្ទុកអគ្គិសនី
មេរៀនទី៤ ៖ រេស៊ីស្តង់អគ្គិសនី
១. រេស៊ីស្តង់អគ្គិសនី
- រេស៊ីស្តង់នៃអង្គធាតុចម្លង គឺជាសមត្ថភាពរបស់ អង្គធាតុក្នុងការប្រឆាំងទប់ទល់ទៅនឹងការចម្លងចរន្តអគ្គិសនី ឬ មានតួនាទីតម្រូវចរន្តអគ្គិសនី ។ អង្គធាតុទាំងអស់មិនមានរេស៊ីស្តង់ដូចៗគ្នាទេ វាអាស្រ័យនឹងប្រវែងអង្គធាតុមុខកាត់ខ្សែចម្លងព្រមទាំងលក្ខណៈទប់ទល់នឹងការចម្លងចរន្តរបស់អង្គធាតុនីមួយៗ។
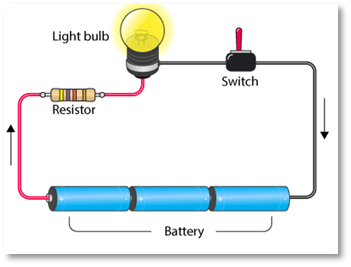
រេស៊ីស្តង់អគ្គិសនី
- បញ្ញត្តិរូបមន្ត៖ រេស៊ីស្តង់នៃអង្គធាតុចម្លង \( \left( R \right) \) អាស្រ័យនឹងប្រភេទខ្សែចម្លង \( \left( \rho \right) \) សមាមាត្រនឹងប្រវែងខ្សែចម្លង \( \left( \ell \right) \) ហើយច្រាសសមាមាត្រនឹងមុខកាត់នៃខ្សែចម្លង (\( A \)) ។
- គេអាចសរសេរ ៖ \( R=\rho \frac{\ell }{A} \)
- ដែល \( R: \) រេស៊ីស្តង់អគ្គិសនី គិតជា \( \left( \Omega \right) \) អូម
\( \rho : \) រេស៊ីស្ទីវីតេនៃអង្គធាតុចម្លង(កម្រិតប្រឆាំងទប់ទល់នឹងការចម្លងចរន្តអគ្គិសនី)គិតជា \( \left( \Omega \cdot \text{m} \right)\ \) អូមម៉ែត្រ
\( \ell : \) ប្រវែងអង្គធាតុចម្លង គិតជា \( \left( \text{m} \right) \) ម៉ែត្រ
\( A: \) ផ្ទៃមុខកាត់ខ្សែចម្លង គិតជា \( \left( {{\text{m}}^{\text{2}}} \right) \) ម៉ែត្រការេ
- ចំណាំ៖ ផ្ទៃមុខកាត់រាងជារង្វង់ \( A=\pi {{r}^{2}};A=\pi \frac{{{D}^{2}}}{4} \)
- ដែល \( r: \) កាំរង្វង់ គិតជា \( \left( \text{m} \right) , D: \) អង្កត់ផ្ចិត គិតជា \( \left( \text{m} \right) \)
- ឧទាហរណ៍៖ ខ្សែចម្លងអគ្គិសនីមួយធ្វើអំពីទង់ដែងមានប្រវែង \( \ell =50\text{cm} \)និងមានអង្កត់ផ្ចិត \( D=2\text{mm} \) ហើយរេស៊ីស្ទីវីតេស្មើនឹង \( \rho =1.7\times {{10}^{-8}}\Omega \text{m} \) ។ គណនារេស៊ីស្តង់នៃខ្សែចម្លងនោះ។
- ដំណោះស្រាយ៖ គណនារេស៊ីស្តង់នៃខ្សែចម្លង R
តាមរូបមន្ត \( R=\rho \frac{\ell }{A} \)
ដោយ \( \rho =1.7\times {{10}^{-8}}\Omega \text{m,}\ell \text{=50cm=50 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{m} \)
- រកផ្ទៃមុខកាត់ \( A \)
តាមរូបមន្ត \( A=\pi \frac{{{D}^{2}}}{4} \)
ដោយ \( D=2\text{mm}=2\times {{10}^{-3}}\text{m},\pi =3.14 \)
គេបាន \( A=3.14\times \frac{{{\left( 2\times {{10}^{-3}} \right)}^{2}}}{4}=3.14\times \frac{4\times {{10}^{-6}}}{4}=3.14\times {{10}^{-6}}{{\text{m}}^{2}} \)
នាំឱ្យ \( R=1.7\times {{10}^{-8}}\times \frac{1}{3.14\times {{10}^{-6}}}=\frac{1.7\times 1}{3.14}\times {{10}^{-8+6}}=0.54\times {{10}^{-2}}\Omega \)
ដូចនេះ \( R=0.54\times {{10}^{-2}}\Omega \)
១.១. រេស៊ីស្តរ និងរេអូស្តា
ក. រេស៊ីស្តរ គឺជាគ្រឿងអគ្គិសនីដែលមានរេស៊ីស្តង់កំណត់។ គេប្រើវានៅក្នុងឧបករណ៍ ដូចជា វិទ្យុ ទូរទស្សន៍ ម៉ាញ៉េ ទូរស័ព្ទ... ដើម្បីកាត់បន្ថយ អាំងតង់ស៊ីតេចរន្តតាមតម្រូវការដែលគេចង់បាន។
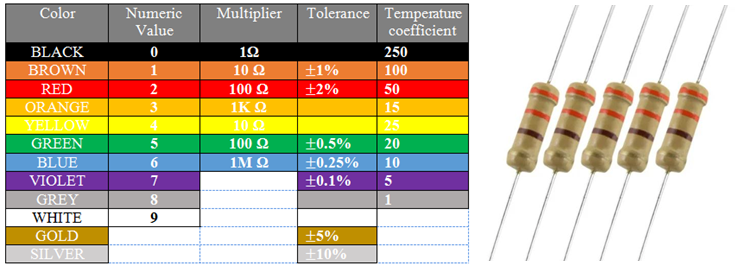
រេស៊ីស្តង់ដែលប្រើក្នុងគ្រឿងអគ្គិសនីមួយចំនួន
ខ. រេអូស្តា គឺជាឧបករណ៍អគ្គិសនីដែលមានរេស៊ីស្តង់អាចប្រែប្រួលបាន។ ហើយគេច្រើនប្រើវានៅ ក្នុងវិទ្យុ ទូរទស្សន៍ ម៉ាញ៉េ កង្ហារ ...ដើម្បីធ្វើឱ្យអាំងតង់ស៊ីតេចរន្តប្រែប្រួលដោយកែប្រែរេស៊ីស្តង់របស់វា។
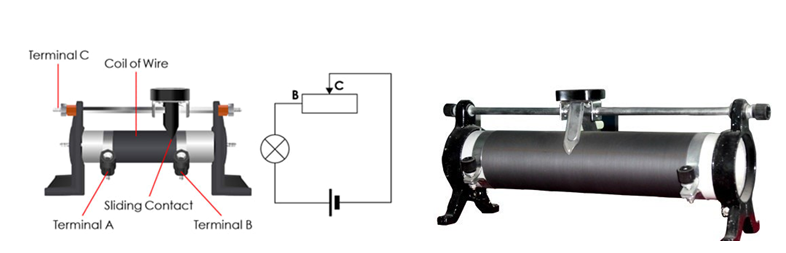
គំនូសបំប្រួញរេអូស្តា និង រេអូស្តា
២. រង្វាស់រេស៊ីស្តង់-ច្បាប់អូម
- ដើម្បីវាស់រេស៊ីស្តង់នៃអង្គធាតុចម្លង យើងត្រូវប្រើច្បាប់អូម ក្នុងនោះ យើងប្រើអំពែម៉ែត្រតជាស៊ែរីនឹងអង្គធាតុ ដើម្បីវាស់អាំងតង់ស៊ីតេចរន្តអគ្គិសនី ដែលបានឆ្លងកាត់។ ហើយប្រើវ៉ុលម៉ែត្រតជាខ្នែង ដើម្បីវាស់ផលសងប៉ូតង់ស្យែល ឬតង់ស្យុងរបស់អង្គធាតុចម្លង។
- ច្បាប់អូម អាំងតង់ស៊ីតេចរន្តឆ្លងកាត់អង្គធាតុចម្លងមួយសមាមាត្រនឹងតង់ស្យុងរវាងចុងសងខាង នៃអង្គធាតុចម្លងនោះ ហើយច្រាសសមាមាត្រនឹងរេស៊ីស្តង់របស់វា។
- គេអាចសរសេរ៖ \( I=\frac{V}{R} \)
ដែល \( R: \) រេស៊ីស្តង់នៃអង្គធាតុចម្លង គិតជា \( \left( \Omega \right) \) អូម
\( V: \) តង់ស្យុង ឬផលសងប៉ូតង់ស្យែលអគ្គិសនី គិតជា \( \left( V \right) \) វ៉ុល
\( I \) : អាំងតង់ស៊ីតេចរន្តអគ្គិសនី គិតជា \( \left( \text{A} \right) \) អំពែ
ពេលគេសួររកតង់ស្យុងអគ្គិសនី៖ \( I=\frac{V}{R}\Rightarrow V=RI \)
ពេលគេសួររករេស៊ីស្តង់អគ្គិសនី៖ \( I=\frac{V}{R}\Rightarrow R=\frac{V}{I} \)
ឧទាហរណ៍៖ ក្នុងសៀគ្វីមួយមានចង្កៀងអគ្គិសនីតជាស៊េរីជាមួយអំពែម៉ែត្រមួយ។ តម្លៃអំពែម៉ែត្រចង្អុលតម្លៃលេខ \( I=0.35\text{A} \) ហើយតង់ស្យុងរវាងចុងសងខាងនៃចង្កៀងស្មើនឹង \( V=3.5\text{V} \)។ គណនារេស៊ីស្តង់នៃចង្កៀងនោះ។
ដំណោះស្រាយ៖ គណនារេស៊ីស្តង់ R
តាមរូបមន្ត \( I=\frac{V}{R}\Rightarrow R=\frac{V}{I} \)
ដោយ \( I=0.35\text{A},V=3.5\text{V}\ \)
គេបាន \( R=\frac{3.5}{0.35}=10\Omega \)
ដូចនេះ \( R=10\Omega \)