(ជ៤)មេរៀនទី៣៖ (សង្ខេបមេរៀន) រង្វាស់សម្ពាធនៃអង្គធាតុរាវ

ជំពូកទី​៤ ៖ សម្ពាធ

មេរៀនទី៣ ៖ រង្វាស់សម្ពាធនៃអង្គធាតុរាវ

១.ម៉ាណូម៉ែត្រ

- ម៉ាណូម៉ែត្រ គឺជាឧបករណ៍សម្រាប់វាស់អង្គធាតុរាវ។

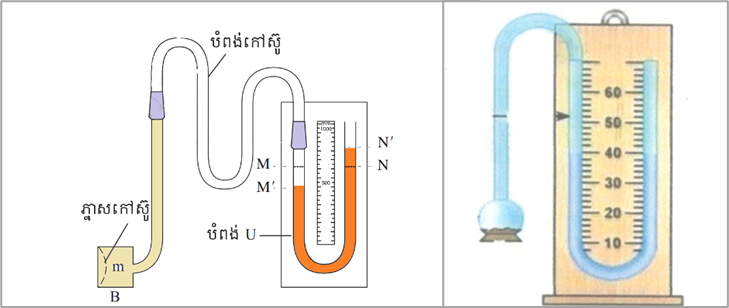
ឧបករណ៍ម៉ាណូម៉ែត្រ

២.សម្ពាធក្នុងអង្គធាតុរាវ

២.១.សម្ពាធក្នុងអង្គធាតុត្រង់ចំណុចណាមួយ

- សម្ពាធក្នុងអង្គធាតុរាវត្រង់ចំណុចមួយ មានតម្លៃស្មើគ្នានៅគ្រប់ទិស។

២.២.សម្ពាធក្នុងអង្គធាតុរាវនៅជម្រៅស្មើគ្នា

- ជម្រៅស្មើគ្នា នោះសម្ពាធនៃអង្គធាតុរាវមានតម្លៃស្មើគ្នា។

២.៣.សម្ពាធក្នុងអង្គធាតុរាវកើនឡើងតាមជម្រៅ

- កាលណាជម្រៅអង្គធាតុរាវកាន់តែជ្រៅ នោះសម្ពាធរបស់វាក៏កាន់តែធំផងដែរ។ 

២.៤.សម្ពាធក្នុងអង្គធាតុរាវអាស្រ័យនឹងម៉ាសមាឌ

- កាលណាអង្គធាតុមានម៉ាសមាឌធំ នោះសម្ពាធអង្គធាតុរាវក៏ធំដែរ (ករណីជម្រៅអង្គធាតុពីរស្មើគ្នា)។

- ដើម្បីដឹងពីម៉ាសមាឌនៃអង្គធាតុរឹង​ រាវ ឬឧស្ម័ណាមួយ អ្នកត្រូវកំណត់ទំហំពីរគឺ ម៉ាស និងមាឌ របស់អង្គធាតុនោះ។ ម៉ាសមាឌ ជាទំហំនៃអង្គធាតុមួយដែលអាចឱ្យយើងដឹងថា អង្គធាតុនោះមានម៉ាសប៉ុន្មានគឺឡូក្រាមក្នុងមួយម៉ែត្រគូប មានន័យថា ជាផលធៀបរវាងម៉ាសនិងមាឌនៃអង្គធាតុនោះ។

- គេបាន រូបមន្ត ៖ \( \rho =\frac{m}{V} \)

ដោយ

• • • • m : ម៉ាស គិតជា kg
      • V : មាឌ គិតជា m³
      • ^{ρ  : ម៉ាសមាឌ គិតជា kg/m3}

· ម៉ាសទឹក \( 1Kg \) មានមាឌ \( 1L \)

· ម៉ាសទឹក \( 10Kg \)មានមាឌ \( 10L \)

· ម៉ាសទឹក \( 100Kg \) មានមាឌ \( 100L \)

· ម៉ាសទឹក \( 1000Kg \) មានមាឌ \( 1000L \)

- តាមរូបមន្តខាងលើ គេអាចកំណតើម៉ាសមាឌទឹក

យើងបាន  ៖ \( \rho =\frac{m}{V}=\frac{1000Kg}{1000L}=\frac{1000Kg}{1000{{m}^{3}}}=\frac{1000Kg}{1{{m}^{3}}}=1000Kg/{{m}^{3}} \)

៣.សម្ពាធអង្គធាតុរាវនៅជម្រៅណាមួយ(មិនគិតសម្ពាធបរិយាកាស)

- គេអាចគណនាសម្ពាធត្រង់ចំណុចណាមួយក្នុងអង្គធាតុរាវដោយស្គាល់ម៉ាស មាឌ និងជម្រៅនៃអង្គធាតុរាវនោះ។

- សម្ពាធអង្គធាតុរាវ = ម៉ាសមាឌ \( \times \) សំទុះទំនាញផែនដី \( \times \) ជម្រៅឬកម្ពស់នៃអង្គធាតុ

- តាមរូបមន្ត \( P=\rho gh \)

• • •  \( \rho \) : ម៉ាសមាឌ គិតជា \( Kg/{{m}^{3}} \)

\( \Rightarrow \): ជម្រៅ ឬកម្ពស់អង្គធាតុរាវ គិតជា \( c{{m}^{2}} \)

• • •  \( P \) : សម្ពាធ គិតជា \( (N/{{m}^{2}} \) ឬ \( Pa) \)

- ឧទាហរណ៍:  ទឹកក្នុងអាងមួយមានជម្រៅ  \( 2m \) បើគេដឹងថាម៉ាសមាឌរបស់ទឹកគឺ \( \rho =1000Kg/{{m}^{3}} \)។
គណនាសម្ពាធនៅបាតអាង។សំទុះទំនាញផែនដីស្មើនឹង \( 10N/Kg \) ។

-ដំណោះស្រាយ

គណនាសម្ពាធនៅបាតអាង

តាមរូបមន្ត \( P=\rho gh \)

ដោយ \( \rho=1000Kg/{{m}^{3}} \), \( g= 10N/Kg \), \( h = 2m \)

យើងបាន \( P= 1000Kg/{{m}^{3}}\times 10N/Kg\times2m= 20 000N/{{m}^{2}} \)

- លំហាត់គំរូទី1 ៖ គណនាសម្ពាធទឹកទៅលើអង្គធាតុរឹងមួយដែលមានផ្ទៃបាត \( 1c{{m}^{2}} \) ហើយឋិតនៅជម្រៅ \( 5cm \) ពីផ្ទៃស្រឡះនៃទឹក។គេឱ្យម៉ាសមាឌទឹក \( 1000Kg/{{m}^{3}} \) និង \( g= 10N/Kg \)។

- ដំណោះស្រាយ

- គណនាសម្ពាធនៅបាតអាង

តាមរូបមន្ត \( P=\rho gh \)

ដោយ \( \rho =1000Kg/{{m}^{3}} \) , \( g= 10N/Kg \), \( h = 5cm= 0.05m \)

យើងបាន \( P= 1000Kg/{{m}^{3}}\times 10N/Kg\times 0.05m= 500N/{{m}^{2}} \)

ដូចនេះ សម្ពាធនៅបាតអាងគឺ P = 500N/m²

- លំហាត់គំរូទី2 :  ឥឡូវនេះគេយកបារតមកជំនួសទឹកវិញម្តង​ តើសម្ពាធបារតមានទៅលើផ្ទៃបាតនៃអង្គធាតុរឹងនៅជម្រៅជម្រៅ \( 5cm \) ស្មើនឹងប៉ុន្មាន?គេឱ្យម៉ាសមាឌបារត \( 13600Kg/{{m}^{3}}និង g= 10N/Kg \)។

- ដំណោះស្រាយ

គណនាសម្ពាធនៅបាតអាង

តាមរូបមន្ត $P=\rho gh$

ដោយ \( \rho =13​ 600Kg/{{m}^{3}}, g= 10N/Kg, h = 5cm= 0.05m \)

យើងបាន \( P= 13 600Kg/{{m}^{3}}\times 10N/Kg\times 0.05m= 6 800N/{{m}^{2}} \)

ដូចនេះ សម្ពាធនៅបាតអាងគឺ P = 6800N/m²

សម្គាល់ :  សម្ពាធនៃអង្គធាតុនៅជម្រៅណាមួយគឺ \( P=\rho gh \) បញ្ជាក់ថា “សម្ពាធក្នុងអង្គធាតុរាវ កើនឡើងតាមជម្រៅ និងប្រែប្រួលទៅតាមម៉ាសមាឌនៃអង្គធាតុរាវនោះ ”។

- ករណីគេសួររកជម្រៅ \( P=\rho gh\Rightarrow h=\frac{P}{\rho g} \)

៤.ការអនុវត្ត

- កាលណាជម្រៅកាន់តែជ្រៅនោះសម្ពាធនៃទឹកក៏កាន់តែធំបាន ដូច្នេះគេត្រូវសង់ផ្ទៃខាងរបស់ទំនប់ទឹកឱ្យធំ ហើយកោងបន្តិច និងពង្រីកបាតវាឱ្យក្រាស់ផងដែរ។